Complex contour of a pendulum

complex surface of a Hamiltoanian

\[H(q, p) = \frac{p^2}{2} + k \cos q\]

with \(Re[E]=const.\)

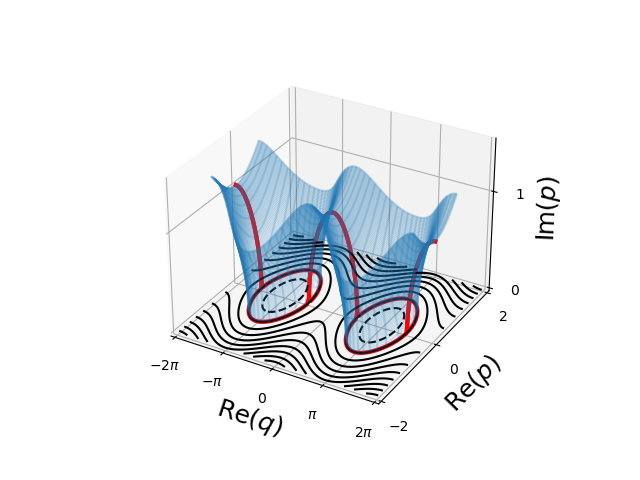
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

np.seterr(invalid='ignore')


twopi = 2*np.pi
x = np.linspace(-twopi,twopi,100)
y = np.linspace(-2,2,100)

x,y = np.meshgrid(x,y)
eps = 0.5
Ham = lambda q,p: p**2/2 + eps*np.cos(q)

#fig, ax = plt.subplots(1,1,projection="3d")
fig = plt.figure()
fig.patch.set_visible(0)
ax = fig.add_subplot(1,1,1,projection="3d")
ax.patch.set_alpha(0)

ax.contour(x,y,Ham(x,y),10,zdir='z',offset=0,colors="k")
E=0
def P(q,E):
    return np.sqrt(2*(E-eps*np.cos(q)))

twopi = 2*np.pi
q = np.linspace(-twopi,twopi,2000) + 0.j
p = P(q,E)
ax.plot(q.real, p.real, p.imag, "-r",lw=3)
ax.plot(q.real, -p.real, p.imag, "-r",lw=3)

sample=100
E=0 + np.linspace(0,1,sample)*1.j
q = np.linspace(-twopi,twopi,sample) + 0.j
q,E=np.meshgrid(q,E)
p = P(q,E)
ax.plot_wireframe(q.real,p.real,p.imag,alpha=0.2)
ax.plot_wireframe(q.real,-p.real,p.imag,alpha=0.2)
ax.set_zlim(0,1.5)
ax.set_xlim(-twopi,twopi)
ax.set_ylim(-2,2)
ax.set_xlabel("$\mathrm{Re}(q)$",fontsize=18)
ax.set_ylabel("$\mathrm{Re}(p)$",fontsize=18)
ax.set_zlabel("$\mathrm{Im}(p)$",fontsize=18)
ax.set_xticks([-twopi, -np.pi, 0,np.pi, twopi])
E=0
q0=np.arccos(2*E/eps)
#ax.text(q0,0,0,r"$a$", fontsize=15,bbox=dict(facecolor='w', edgecolor='none', pad=0,alpha=1))
#ax.text(-q0,0,0,r"$-a$",fontsize=15,bbox=dict(facecolor='w', edgecolor='none', pad=0,alpha=0.8))
ax.set_yticks([-2,0,2])
ax.set_zticks([0,1])
ax.set_xticklabels([r"$-2\pi$", r"$-\pi$", r"$0$", r"$\pi$", r"$2\pi$"])
#plt.tight_layout()
#plt.savefig("complex_pen.svg")
plt.show()