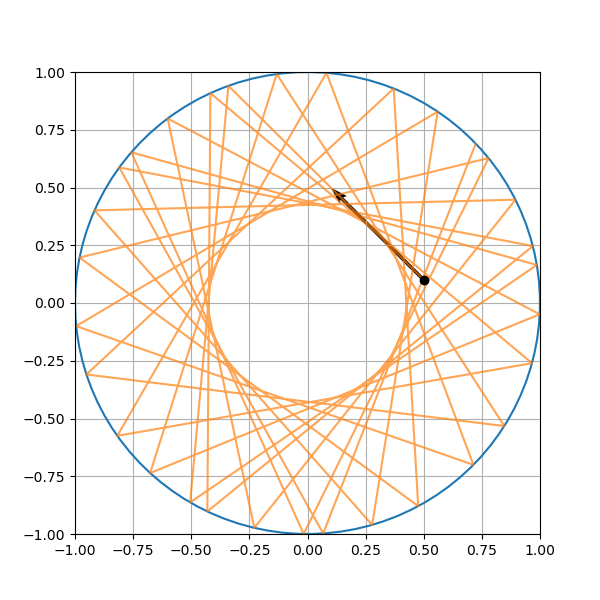
(classical) circular billard

import numpy as np
import matplotlib.pyplot as plt

fig, ax = plt.subplots(1,1, figsize=(6,6))

theta = np.linspace(-np.pi, np.pi, 100)
z = np.exp(1j*theta)
ax.plot(z.real, z.imag, '-')
ax.set_xlim(-1,1)
ax.set_ylim(-1,1)

def df(x):
    return np.array([2*x[0], 2*x[1]])

def intersection(vec0, coord):
    a = vec0[1]/vec0[0]
    if np.abs(a) > 1e7:
        z = np.array([x1, -y0])

    x0 = coord[0]
    y0 = coord[1]
    sg = np.sign(vec0[0])
    D = 1 - a**2*(-1+x0**2)+ 2*a*x0*y0 -y0**2
    x1 = - ( -a**2*x0 + a*y0 - sg * np.sqrt(D) ) / (1 + a**2)

    y1 = (y0 -a * ( x0 - sg* np.sqrt(D) ) )/ (1 + a**2)
    z = np.array([x1, y1])
    return z

#x0 = np.array([0, 1/np.sqrt(2)])
x0 = np.array([0.5, 0.1])
vec0 = np.array([-0.2, 0.2])

ini_x0 = x0.copy()
ini_vec0 = vec0.copy()

x1 = intersection(vec0, x0)

traj = [np.array([]), np.array([])]

traj[0] = np.append(traj[0], x0[0])
traj[1] = np.append(traj[1], x0[1])

traj[0] = np.append(traj[0], x1[0])
traj[1] = np.append(traj[1], x1[1])

n = -df(x1)
pn = -np.dot(vec0, n)/np.dot(n, n) * n
vec1 = vec0 + 2*pn

#ax.quiver(x1[0], x1[1], n[0], n[1], angles='xy', scale_units='xy', scale=10)
#ax.quiver(x1[0], x1[1], vec1[0], vec1[1], angles='xy', scale_units='xy', scale=1)

for n in range(30):
    x0 = x1.copy()
    vec0 = vec1.copy()

    x1 = intersection(vec0, x0)
    traj[0] = np.append(traj[0], x1[0])
    traj[1] = np.append(traj[1], x1[1])

    n = -df(x1)
    pn = -np.dot(vec0, n)/np.dot(n, n) * n
    vec1 = vec0 + 2*pn

    xx = np.linspace(x0[0], x1[0], 2)
    yy = vec0[1]/vec0[0]*(xx - x0[0]) + x0[1]


ax.plot(traj[0], traj[1],'-', alpha=0.7)

ax.plot(ini_x0[0], ini_x0[1], 'ok')
ax.quiver(ini_x0[0], ini_x0[1], ini_vec0[0], ini_vec0[1], angles='xy', scale_units='xy', scale=0.5)


ax.grid()
plt.show()