Projection and rejection of a vector (2D)

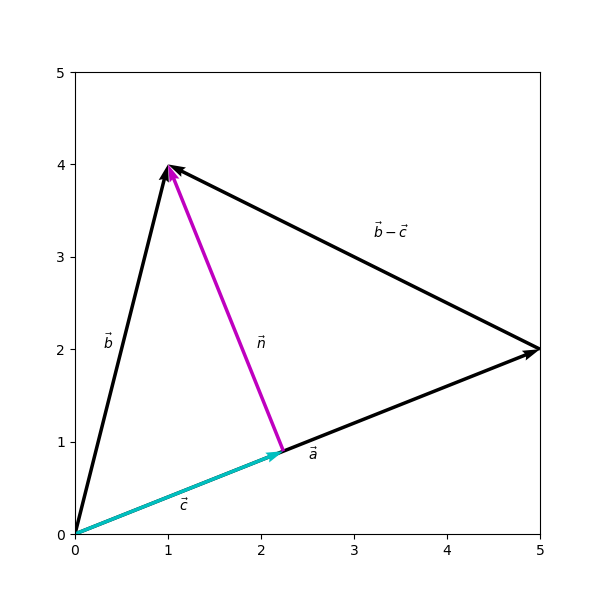
For a given \(\vec{a}\) and \(\vec{b}\),

\[\vec{c} = \frac{\langle \vec{a}, \vec{b}\rangle}{\langle \vec{a}, \vec{a}\rangle }\vec{a}, \qquad \vec{n} = \vec{b} - \vec{c}, \qquad \text{where } \langle \cdot, \cdot\rangle \text{ is a inner product.}\]

import numpy as np
import matplotlib.pyplot as plt

fig, ax = plt.subplots(1,1, figsize=(6,6))


a = np.array([5,2])
b = np.array([1,4])
ba = b -a
c = np.dot(a,b)/np.dot(a,a) * a
n = b - c

tdx = 0.2
plt.quiver(0,0, a[0],a[1], color='k',angles='xy', scale_units='xy', scale=1)#, label=r"$\mathbf{a}$")
ax.text(a[0]/2, a[1]/2-tdx, r"$\vec{a}$")

plt.quiver(0,0, b[0], b[1], color='k',angles='xy', scale_units='xy', scale=1)
ax.text(b[0]/2 - tdx, b[1]/2, r"$\vec{b}$")

plt.quiver(a[0],a[1], ba[0],ba[1], color='k',angles='xy', scale_units='xy', scale=1)
ax.text((b[0]+a[0])/2 + tdx , (b[1]+a[1])/2 + tdx, r"$\vec{b} - \vec{c}$")


plt.quiver(0,0, c[0], c[1], color="c",angles='xy', scale_units='xy', scale=1)
ax.text(c[0]/2, c[1]/2 -tdx, r"$\vec{c}$")

plt.quiver(c[0], c[1], n[0], n[1], color="m",angles='xy', scale_units='xy', scale=1)
ax.text((c[0] - n[0])/2 + tdx, (c[1] + n[1])/2, r"$\vec{n}$")


ax.set_xlim(0,5)
ax.set_ylim(0,5)
plt.show()