download notebook

記述統計

データの要約

次のようなデータが与えられたとする．

\[X = [4, 0, 7, 6, 5, 6, 5, 4, 4, 4, 4, 4, 5, 5, 5, 5, 6, 6, 6, 5, 4, 5, 10],\]

\[Y = [9, 6, 1, 6, 5, 10, 3, 2, 7, 2, 5, 8, 7, 6, 1, 8, 4, 5, 4, 0, 9, 3, 4]\]

データを眺めていても傾向は読めないので，np.sort関数を使ってデータを順に並べてみる

In:

import numpy as np
X = np.array([4, 1, 7, 6, 5, 6, 5, 4, 4, 3, 4, 4, 5, 5, 5, 5, 6, 6, 6, 5, 4, 5, 10])
Y = np.array([9, 6, 1, 6, 5, 10, 3, 2, 7, 2, 5, 8, 7, 6, 1, 8, 4, 5, 4, 0, 9, 3, 4])
print("X :=", np.sort(X) )
print("Y :=", np.sort(Y) )

X := [ 1  3  4  4  4  4  4  4  5  5  5  5  5  5  5  5  6  6  6  6  6  7 10]
Y := [ 0  1  1  2  2  3  3  4  4  4  5  5  5  6  6  6  7  7  8  8  9  9 10]

すると最小値や最大値が一目でわかり

In:

print( np.min(X), np.max(X) ) # = X.max(), X.min()
print( np.min(Y), np.max(Y) ) # = Y.max(), Y.min()

1 10
0 10

もう少し詳しい情報をpandasパッケージを用いて要約させると

In:

import pandas as pd
df = pd.DataFrame({
'試験X': X,
'試験Y': Y,
})
df.describe()

	試験X	試験Y
count	23.000000	23.000000
mean	5.000000	5.000000
std	1.651446	2.796101
min	1.000000	0.000000
25%	4.000000	3.000000
50%	5.000000	5.000000
75%	6.000000	7.000000
max	10.000000	10.000000

とわかる．mean以下の詳細は次節で詳細に説明するが，ここではdf.discribe()の出力結果を簡潔に説明する．

まず，countはデータセットの大きさ（要素数，総度数）であり試験X，試験Yともに23個である． meanはデータセットの平均値であり試験X，試験Yともに5点である． stdは標準偏差であり，試験Xは約1.65点，試験Yは約2.80点である． 標準偏差はデータの散らばりを表す指標（散布度）であり，値が大きいほどデータのばらつきが大きいことを意味し，試験Yの方がデータが散らばっていうることがわかる（逆に試験Xは平均値の周りにデータが集まっている）． minはデータセットの最小値， 25%，50%，75% はデータセットの25%点，50%点（中央値），75%点， maxはデータセットの最大値を意味する． このようにデータセットの特徴量を要約することで，データの傾向を把握することができる．

代表値

In:

n = len(X)
print("平均値 :", np.sum(X) / n )
print("平均値 :", np.mean(X) )

平均値 : 5.0
平均値 : 5.0

In:

X = np.array([50, 100, 150, 200, 4500])
print("平均値：", np.mean(X) )
print("中央値：", np.median(X) )

平均値： 1000.0
中央値： 150.0

散布度

平均偏差

In:

X = np.array([4, 1, 7, 6, 5, 6, 5, 4, 4, 3, 4, 4, 5, 5, 5, 5, 6, 6, 6, 5, 4, 5, 10])
Dx = X - X.mean()
print("Dx = ", Dx)
print("np.mean(Dx) = ", np.mean(Dx) )

Dx =  [-1. -4.  2.  1.  0.  1.  0. -1. -1. -2. -1. -1.  0.  0.  0.  0.  1.  1.
  1.  0. -1.  0.  5.]
np.mean(Dx) =  0.0

問 Yのデータセットに対して同様に偏差の平均値が0になることを示せ．

In:

Y = np.array([9, 6, 1, 6, 5, 10, 3, 2, 7, 2, 5, 8, 7, 6, 1, 8, 4, 5, 4, 0, 9, 3, 4])

２乗偏差と分散・標準偏差

In:

X = np.array([4, 1, 7, 6, 5, 6, 5, 4, 4, 3, 4, 4, 5, 5, 5, 5, 6, 6, 6, 5, 4, 5, 10])
Dx = X - X.mean() # = [𝑑_1, ... , 𝑑_𝑛] where 𝑑𝑖 = (𝑥_𝑖 - 𝑥)
Dx2 = Dx ** 2 # = [𝑑^2_1 , ... ,𝑑^2_𝑛] where 𝑑^2_𝑖 = (𝑥_𝑖 - 𝑥)^2
print("Dx2 = ", Dx2)
print("np.mean(Dx2) = ", np.mean(Dx2) )

Dx2 =  [ 1. 16.  4.  1.  0.  1.  0.  1.  1.  4.  1.  1.  0.  0.  0.  0.  1.  1.
  1.  0.  1.  0. 25.]
np.mean(Dx2) =  2.608695652173913

In:

print( X.var() )

2.608695652173913

問 Yのデータセットに対して同様に２乗偏差の平均値を求め，np.var(Y)の値と一致することを示せ．

In:

print("std = ", np.sqrt( np.var(X) ))

std =  1.6151457061744965

In:

print(r"std = ", np.std(X) ) # = X.std()

std =  1.6151457061744965

In:

X2 = X**2

分散の計算公式

\(s^2 = \overline{(x^2)} - \overline{(x)}^2\)から分散の値を求める．

In:

X = np.array([4, 1, 7, 6, 5, 6, 5, 4, 4, 3, 4, 4, 5, 5, 5, 5, 6, 6, 6, 5, 4, 5, 10])
X2 = X ** 2 # $= [4^2, 1^2, ..., 5^2, 10^2]$
s2 = np.mean(X2) - np.mean(X) ** 2 # $= ¥overline{(x^2)} - (¥overline{x})^2$
print( s2 )
print( X.var() )

2.608695652173914
2.608695652173913

問 データセット\(Y\)に対して同様に，\(Y^2\)のデータセットを作成し，分散の計算公式から分散\(s^2\)を評価せよ．またその値がnp.var(Y)の値に一致することを確認せよ．

データの整理

名義尺度の場合

In:

import pandas as pd
import numpy as np
X = ["A", "B", "O", "A", "O", "AB", "B", "O", "A", "O",
     "A", np.nan, "B", "AB", "O", "O", "A", "O", "B", "AB", "O"]
bloodtypes = pd.Series(X)
print("unique dataset =", bloodtypes.unique() )
print("総度数 =", bloodtypes.count() )
print("Xの大きさ = ", len(X) )

unique dataset = ['A' 'B' 'O' 'AB' nan]
総度数 = 20
Xの大きさ =  21

In:

bloodtypes = pd.Series(X).dropna()
print("unique dataset =", bloodtypes.unique() )

unique dataset = ['A' 'B' 'O' 'AB']

In:

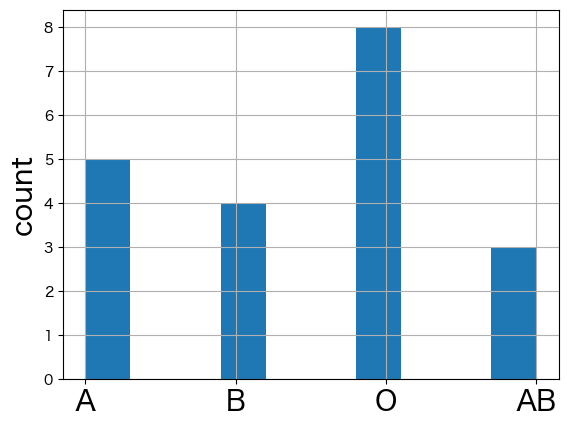
bloodtypes.value_counts().reindex(["A", "B", "O", "AB"])

A     5
B     4
O     8
AB    3
Name: count, dtype: int64

In:

import matplotlib.pyplot as plt
plt.ylabel("count", fontsize=20)
bloodtypes.hist(xlabelsize=20)

<Axes: ylabel='count'>

In:

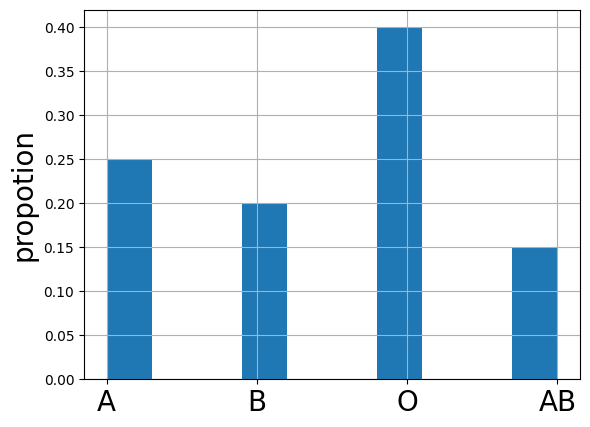
bloodtypes.value_counts(normalize=True).reindex(["A", "B", "O", "AB"])

	proportion
A	0.25
B	0.20
O	0.40
AB	0.15

dtype: float64

In:

n = bloodtypes.count()
w = np.ones(n) / n
print(w)

[0.05 0.05 0.05 0.05 0.05 0.05 0.05 0.05 0.05 0.05 0.05 0.05 0.05 0.05
 0.05 0.05 0.05 0.05 0.05 0.05]

In:

plt.ylabel("propotion",fontsize=20)
bloodtypes.hist(weights=w, xlabelsize=20)

<Axes: ylabel='propotion'>

量的データかつ離散データの場合

In:

data = np.array([4, 1, 7, 6, 5,  6, 5, 4, 4, 3, 4, 4, 5, 5, 5, 5, 6, 6, 6, 5, 4, 5, 10])
X = pd.Series(data)
X.value_counts()

	count
5	8
4	6
6	5
7	1
1	1
3	1
10	1

dtype: int64

In:

Xe = np.arange(0, 11) # = [0, 1, ..., 10]
X.value_counts().reindex(Xe)

	count
0	NaN
1	1.0
2	NaN
3	1.0
4	6.0
5	8.0
6	5.0
7	1.0
8	NaN
9	NaN
10	1.0

dtype: float64

In:

X.value_counts().reindex(Xe, fill_value=0)

	count
0	0
1	1
2	0
3	1
4	6
5	8
6	5
7	1
8	0
9	0
10	1

dtype: int64

In:

X.value_counts(normalize=True).reindex(Xe, fill_value=0)

	proportion
0	0.000000
1	0.043478
2	0.000000
3	0.043478
4	0.260870
5	0.347826
6	0.217391
7	0.043478
8	0.000000
9	0.000000
10	0.043478

dtype: float64

In:

Xe = np.arange(0, 11) # 0, 1, ..., 10
X.value_counts(normalize=True).reindex(Xe, fill_value=0).cumsum()

	proportion
0	0.000000
1	0.043478
2	0.043478
3	0.086957
4	0.347826
5	0.695652
6	0.913043
7	0.956522
8	0.956522
9	0.956522
10	1.000000

dtype: float64

In:

import numpy as np
import pandas as pd
data = np.array([4, 1, 7, 6, 5,  6, 5, 4, 4, 3, 4, 4, 5, 5, 5, 5, 6, 6, 6, 5, 4, 5, 10])
X = pd.Series(data)
Xe = np.arange(0, 11) # = [0, 1, ..., 10]
freq_tab = pd.DataFrame({
    '度数': X.value_counts().reindex(Xe, fill_value=0),
    '相対度数': X.value_counts(normalize=True).reindex(Xe, fill_value=0),
    '累積相対度数': X.value_counts(normalize=True).reindex(Xe, fill_value=0).cumsum()
    }, index = Xe)
freq_tab

	度数	相対度数	累積相対度数
0	0	0.000000	0.000000
1	1	0.043478	0.043478
2	0	0.000000	0.043478
3	1	0.043478	0.086957
4	6	0.260870	0.347826
5	8	0.347826	0.695652
6	5	0.217391	0.913043
7	1	0.043478	0.956522
8	0	0.000000	0.956522
9	0	0.000000	0.956522
10	1	0.043478	1.000000

In:

!pip install japanize-matplotlib
import japanize_matplotlib

Requirement already satisfied: japanize-matplotlib in /usr/local/lib/python3.11/dist-packages (1.1.3)
Requirement already satisfied: matplotlib in /usr/local/lib/python3.11/dist-packages (from japanize-matplotlib) (3.10.0)
Requirement already satisfied: contourpy>=1.0.1 in /usr/local/lib/python3.11/dist-packages (from matplotlib->japanize-matplotlib) (1.3.2)
Requirement already satisfied: cycler>=0.10 in /usr/local/lib/python3.11/dist-packages (from matplotlib->japanize-matplotlib) (0.12.1)
Requirement already satisfied: fonttools>=4.22.0 in /usr/local/lib/python3.11/dist-packages (from matplotlib->japanize-matplotlib) (4.58.4)
Requirement already satisfied: kiwisolver>=1.3.1 in /usr/local/lib/python3.11/dist-packages (from matplotlib->japanize-matplotlib) (1.4.8)
Requirement already satisfied: numpy>=1.23 in /usr/local/lib/python3.11/dist-packages (from matplotlib->japanize-matplotlib) (2.0.2)
Requirement already satisfied: packaging>=20.0 in /usr/local/lib/python3.11/dist-packages (from matplotlib->japanize-matplotlib) (24.2)
Requirement already satisfied: pillow>=8 in /usr/local/lib/python3.11/dist-packages (from matplotlib->japanize-matplotlib) (11.2.1)
Requirement already satisfied: pyparsing>=2.3.1 in /usr/local/lib/python3.11/dist-packages (from matplotlib->japanize-matplotlib) (3.2.3)
Requirement already satisfied: python-dateutil>=2.7 in /usr/local/lib/python3.11/dist-packages (from matplotlib->japanize-matplotlib) (2.9.0.post0)
Requirement already satisfied: six>=1.5 in /usr/local/lib/python3.11/dist-packages (from python-dateutil>=2.7->matplotlib->japanize-matplotlib) (1.17.0)

In:

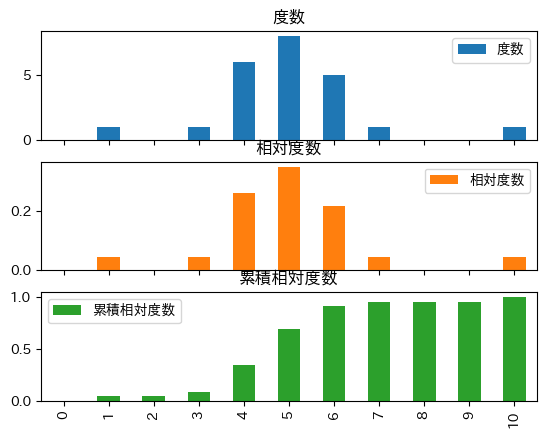
freq_tab.plot(kind='bar', subplots=True)

array([<Axes: title={'center': '度数'}>, <Axes: title={'center': '相対度数'}>,
       <Axes: title={'center': '累積相対度数'}>], dtype=object)

In:

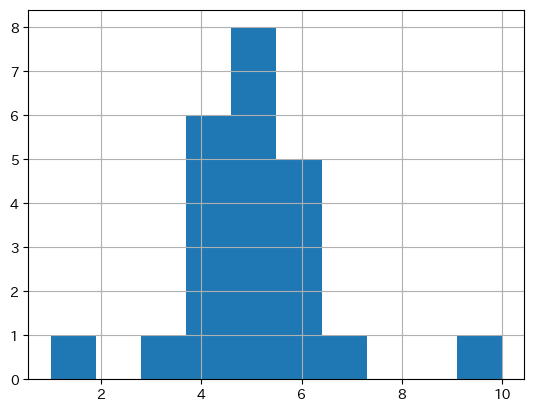
X.hist() # 度数

<Axes: >

In:

w = np.ones(X.count()) / X.count()
X.hist(weights=w) # 相対度数

<Axes: >

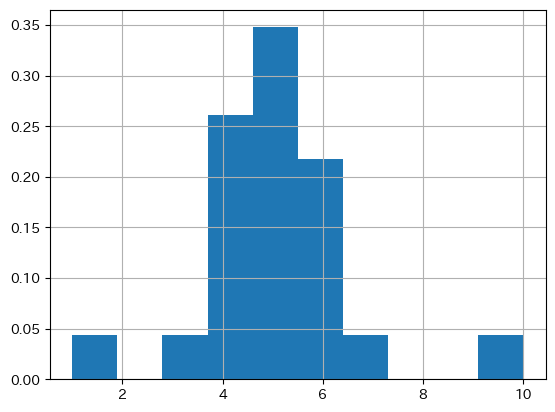
量的データかつ連続データの場合

In:

data = [161.05, 176.75, 167.71, 180.49, 176.56, 165.79, 163.04,
        174.24, 171.99, 172.79, 163.93, 170.52, 173.68, 171.79, 164.07]
X = pd.Series(data)
X.value_counts()

	count
161.05	1
176.75	1
167.71	1
180.49	1
176.56	1
165.79	1
163.04	1
174.24	1
171.99	1
172.79	1
163.93	1
170.52	1
173.68	1
171.79	1
164.07	1

dtype: int64

In:

k = 5 # 階級の数
X.value_counts(bins=k).sort_index() # sort_index()をつけない場合は度数の大きい順に並ぶ

	count
(161.03, 164.938]	4
(164.938, 168.826]	2
(168.826, 172.714]	3
(172.714, 176.602]	4
(176.602, 180.49]	2

dtype: int64

In:

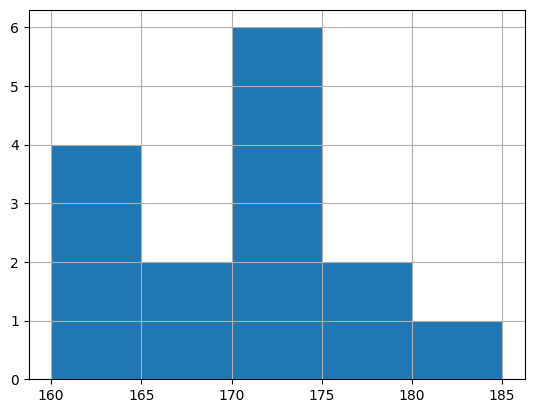
X.value_counts(bins=[160, 165, 170, 175, 180, 185]).sort_index()

	count
(159.999, 165.0]	4
(165.0, 170.0]	2
(170.0, 175.0]	6
(175.0, 180.0]	2
(180.0, 185.0]	1

dtype: int64

In:

import pandas as pd
data = [161.05, 176.75, 167.71, 180.49, 176.56, 165.79, 163.04,
        174.24, 171.99, 172.79, 163.93, 170.52, 173.68, 171.79, 164.07]
X = pd.Series(data)
cls = [160, 165, 170, 175, 180, 185]
freq = X.value_counts(bins=cls).sort_index() # 度数
prop = X.value_counts(bins=cls, normalize=True).sort_index() # 相対度数
cprop = X.value_counts(bins=cls, normalize=True).cumsum().sort_index() # 累積相対度数
freq_tab = pd.DataFrame({
"階級値": freq.index.mid, # 階級区間の中央
"度数": freq,
"相対度数": prop,
"累積相対度数": cprop
}, index=freq.index)
freq_tab

	階級値	度数	相対度数	累積相対度数
(159.999, 165.0]	162.4995	4	0.266667	0.666667
(165.0, 170.0]	167.5000	2	0.133333	0.800000
(170.0, 175.0]	172.5000	6	0.400000	0.400000
(175.0, 180.0]	177.5000	2	0.133333	0.933333
(180.0, 185.0]	182.5000	1	0.066667	1.000000

In:

X.hist(bins = [160, 165, 170, 175, 180, 185])

<Axes: >

度数分布表から平均・分散を求める．

In:

import numpy as np
import pandas as pd
data = np.array([4, 1, 7, 6, 5,  6, 5, 4, 4, 3, 4, 4, 5, 5, 5, 5, 6, 6, 6, 5, 4, 5, 10])
ds = pd.Series(data)
Xe = np.arange(0, 11) # = [0, 1, ..., 10] # 期待しているユニークなデータセット
f = ds.value_counts().reindex(Xe, fill_value=0).to_numpy() #　.to\_numpy()でnumpyの配列に変換
p = ds.value_counts(normalize=True).reindex(Xe, fill_value=0).to_numpy()
print("Xe = ", Xe)
print("f = ", f)
print("p = ", p)

Xe =  [ 0  1  2  3  4  5  6  7  8  9 10]
f =  [0 1 0 1 6 8 5 1 0 0 1]
p =  [0.         0.04347826 0.         0.04347826 0.26086957 0.34782609
 0.2173913  0.04347826 0.         0.         0.04347826]

In:

x = np.array([1, 2, 3])
y = np.array([2, 0, 10])
x * y

array([ 2,  0, 30])

In:

Xe * f

array([ 0,  1,  0,  3, 24, 40, 30,  7,  0,  0, 10])

In:

n = X.count()
mean1 = np.sum( Xe * f ) / n
mean2 = np.sum( Xe * p )
print(mean1, mean2)

5.0 5.0

In:

D2 = ( Xe - X.mean() ) ** 2
D2

array([25., 16.,  9.,  4.,  1.,  0.,  1.,  4.,  9., 16., 25.])

In:

var1 = np.sum( D2 * f) / n
var2 = np.sum( D2 * p )
print(var1, var2)

2.608695652173913 2.608695652173913

In:

Xe2 = Xe * Xe
Xe2

array([  0,   1,   4,   9,  16,  25,  36,  49,  64,  81, 100])

In:

Xe2_mean = np.sum( Xe2 * p )
Xe_mean  = np.sum( Xe * p)
var = Xe2_mean - Xe_mean ** 2
print(var)

2.608695652173914

In:

np.abs(var1 - var)

np.float64(8.881784197001252e-16)

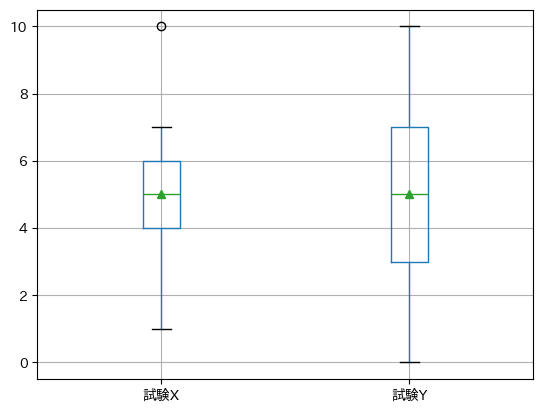
箱ひげ図

In:

!pip install japanize-matplotlib
import japanize_matplotlib

Requirement already satisfied: japanize-matplotlib in /usr/local/lib/python3.11/dist-packages (1.1.3)
Requirement already satisfied: matplotlib in /usr/local/lib/python3.11/dist-packages (from japanize-matplotlib) (3.10.0)
Requirement already satisfied: contourpy>=1.0.1 in /usr/local/lib/python3.11/dist-packages (from matplotlib->japanize-matplotlib) (1.3.2)
Requirement already satisfied: cycler>=0.10 in /usr/local/lib/python3.11/dist-packages (from matplotlib->japanize-matplotlib) (0.12.1)
Requirement already satisfied: fonttools>=4.22.0 in /usr/local/lib/python3.11/dist-packages (from matplotlib->japanize-matplotlib) (4.58.4)
Requirement already satisfied: kiwisolver>=1.3.1 in /usr/local/lib/python3.11/dist-packages (from matplotlib->japanize-matplotlib) (1.4.8)
Requirement already satisfied: numpy>=1.23 in /usr/local/lib/python3.11/dist-packages (from matplotlib->japanize-matplotlib) (2.0.2)
Requirement already satisfied: packaging>=20.0 in /usr/local/lib/python3.11/dist-packages (from matplotlib->japanize-matplotlib) (24.2)
Requirement already satisfied: pillow>=8 in /usr/local/lib/python3.11/dist-packages (from matplotlib->japanize-matplotlib) (11.2.1)
Requirement already satisfied: pyparsing>=2.3.1 in /usr/local/lib/python3.11/dist-packages (from matplotlib->japanize-matplotlib) (3.2.3)
Requirement already satisfied: python-dateutil>=2.7 in /usr/local/lib/python3.11/dist-packages (from matplotlib->japanize-matplotlib) (2.9.0.post0)
Requirement already satisfied: six>=1.5 in /usr/local/lib/python3.11/dist-packages (from python-dateutil>=2.7->matplotlib->japanize-matplotlib) (1.17.0)

In:

import numpy as np
import pandas as pd
X = np.array([4, 1, 7, 6, 5,  6, 5, 4, 4, 3, 4, 4, 5, 5, 5, 5, 6, 6, 6, 5, 4, 5, 10])
Y = np.array([9, 6, 1, 6, 5, 10, 3, 2, 7, 2, 5, 8, 7, 6, 1, 8, 4, 5, 4, 0, 9, 3, 4])
df = pd.DataFrame({
    '試験X': X,
    '試験Y': Y,
})
df.boxplot(showmeans=True) # showmeans=Trueで平均値$\bar{x}$が表示される．

<Axes: >

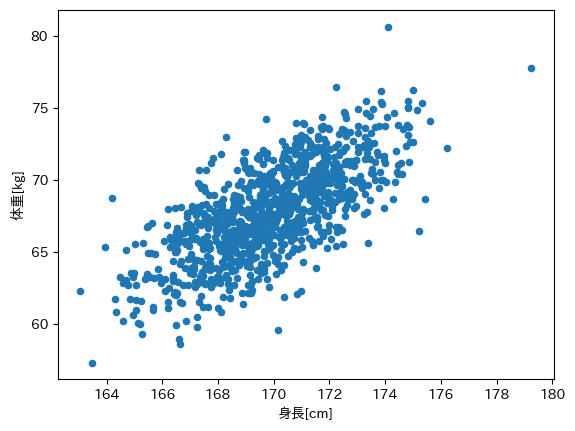
相関

In:

import numpy as np

np.random.seed(8787)

# 平均, 分散, 標準偏差
mean_X, mean_Y = 170, 68
var_X, var_Y = 5, 10
std_X, std_Y  = np.sqrt(var_X), np.sqrt(var_Y)
rho = 0.7  # 相関係数

# 共分散行列
cov = [
    [var_X,               rho * std_X * std_Y],
    [rho * std_X * std_Y, var_Y              ]
]
L = np.linalg.cholesky(cov)

# ランダムな非相関標準正規データを生成
num_samples = 1000
uncorr = np.random.standard_normal( (2, num_samples) )

# 相関のあるデータに変換
mean = np.array([mean_X, mean_Y]).reshape(2, 1)
data = np.dot(L, uncorr) + mean

import pandas as pd

df = pd.DataFrame({
  "身長[cm]": data[0, :],
  "体重[kg]": data[1, :]
 })

In:

print(df.describe())

            身長[cm]       体重[kg]
count  1000.000000  1000.000000
mean    169.841922    67.796619
std       2.267517     3.246836
min     163.060816    57.335005
25%     168.303610    65.626473
50%     169.838044    67.734873
75%     171.444423    70.033005
max     179.247738    80.651467

In:

!pip install japanize-matplotlib
import japanize_matplotlib

Requirement already satisfied: japanize-matplotlib in /usr/local/lib/python3.11/dist-packages (1.1.3)
Requirement already satisfied: matplotlib in /usr/local/lib/python3.11/dist-packages (from japanize-matplotlib) (3.10.0)
Requirement already satisfied: contourpy>=1.0.1 in /usr/local/lib/python3.11/dist-packages (from matplotlib->japanize-matplotlib) (1.3.2)
Requirement already satisfied: cycler>=0.10 in /usr/local/lib/python3.11/dist-packages (from matplotlib->japanize-matplotlib) (0.12.1)
Requirement already satisfied: fonttools>=4.22.0 in /usr/local/lib/python3.11/dist-packages (from matplotlib->japanize-matplotlib) (4.58.4)
Requirement already satisfied: kiwisolver>=1.3.1 in /usr/local/lib/python3.11/dist-packages (from matplotlib->japanize-matplotlib) (1.4.8)
Requirement already satisfied: numpy>=1.23 in /usr/local/lib/python3.11/dist-packages (from matplotlib->japanize-matplotlib) (2.0.2)
Requirement already satisfied: packaging>=20.0 in /usr/local/lib/python3.11/dist-packages (from matplotlib->japanize-matplotlib) (24.2)
Requirement already satisfied: pillow>=8 in /usr/local/lib/python3.11/dist-packages (from matplotlib->japanize-matplotlib) (11.2.1)
Requirement already satisfied: pyparsing>=2.3.1 in /usr/local/lib/python3.11/dist-packages (from matplotlib->japanize-matplotlib) (3.2.3)
Requirement already satisfied: python-dateutil>=2.7 in /usr/local/lib/python3.11/dist-packages (from matplotlib->japanize-matplotlib) (2.9.0.post0)
Requirement already satisfied: six>=1.5 in /usr/local/lib/python3.11/dist-packages (from python-dateutil>=2.7->matplotlib->japanize-matplotlib) (1.17.0)

In:

df.plot(kind='scatter', x='身長[cm]', y='体重[kg]')

<Axes: xlabel='身長[cm]', ylabel='体重[kg]'>

In:

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(87)
ns = 1000 # number of samples

def gen_corr_data(ns, rho):
  # 平均, 分散, 標準偏差
  mean_X, mean_Y = 170, 68
  var_X, var_Y = 5, 10
  std_X, std_Y  = np.sqrt(var_X), np.sqrt(var_Y)
  rho = rho  # 相関係数
  # 共分散行列
  cov = [
      [var_X,               rho * std_X * std_Y],
      [rho * std_X * std_Y, var_Y              ]
  ]
  L = np.linalg.cholesky(cov)

  # ランダムな非相関標準正規データを生成
  uncorr = np.random.standard_normal( (2, num_samples) )

# 相関のあるデータに変換
  mean = np.array([mean_X, mean_Y]).reshape(2, 1)
  data = np.dot(L, uncorr) + mean
  return data

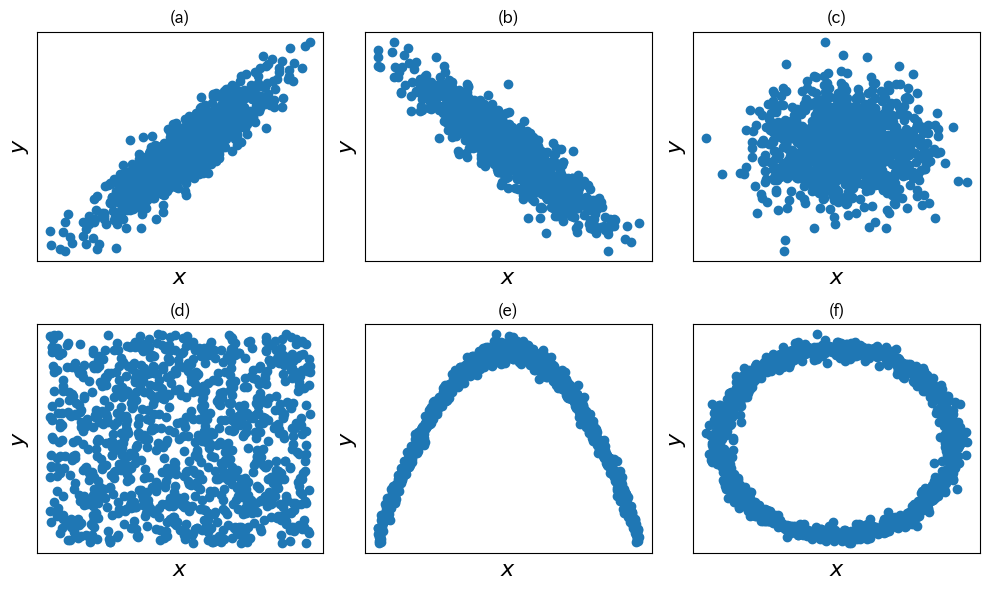
fig, ax = plt.subplots(2, 3, figsize=(10,6))
X1, Y1 = gen_corr_data(ns, 0.9)
X2, Y2 = gen_corr_data(ns, -0.9)
X3, Y3 = gen_corr_data(ns, 0)
X4, Y4 = np.random.random(ns), np.random.random(ns)
x = np.linspace(-10, 10, ns)
eps = np.random.normal(0, 3, ns) # noise
y5 = - x ** 2 + eps
eps = np.random.normal(0, 0.05, ns) # noise
z = (1 + eps)*np.exp( 1.j * 2*np.pi * x)
ax[0,0].scatter(X1, Y1)
ax[0,1].scatter(X2, Y2)
ax[0,2].scatter(X3, Y3)
ax[1,0].scatter(X4, Y4)
ax[1,1].scatter(x, y5)
ax[1,2].scatter(z.real, z.imag)
#ax[3].scatter(z.real, z.imag)
tit=["(a)", "(b)" ,"(c)", "(d)", "(e)", "(f)"]
for i, a in enumerate(ax.flat):
  a.set_xlabel(r"$x$", fontsize=16)
  a.set_ylabel(r"$y$", fontsize=16)
  a.set_title(tit[i])
  a.set_xticks([])
  a.set_yticks([])
plt.tight_layout()

In:

for i,j in